Skip to contents

Decode the underlying hidden state sequence

Source: R/decode_states.R
decode_states.Rd

This function decodes the (most likely) underlying hidden state sequence by applying the Viterbi algorithm for global decoding.

Usage

decode_states(x, verbose = TRUE)

viterbi(observations, nstates, sdd, Gamma, mu, sigma = NULL, df = NULL)

Arguments

x

An object of class fHMM_model.

verbose

Set to TRUE to print progress messages.

observations

A numeric vector of state-dependent observations.

nstates

The number of states.

sdd

A character, specifying the state-dependent distribution. One of

  • "normal" (the normal distribution),

  • "lognormal" (the log-normal distribution),

  • "t" (the t-distribution),

  • "gamma" (the gamma distribution),

  • "poisson" (the Poisson distribution).

Gamma

A transition probability matrix of dimension nstates.

mu

A numeric vector of expected values for the state-dependent distribution in the different states of length nstates.

For the gamma- or Poisson-distribution, mu must be positive.

sigma

A positive numeric vector of standard deviations for the state-dependent distribution in the different states of length nstates.

Not relevant in case of a state-dependent Poisson distribution.

df

A positive numeric vector of degrees of freedom for the state-dependent distribution in the different states of length nstates.

Only relevant in case of a state-dependent t-distribution.

Value

An object of class fHMM_model with decoded state sequence included.

References

https://en.wikipedia.org/wiki/Viterbi_algorithm

Examples

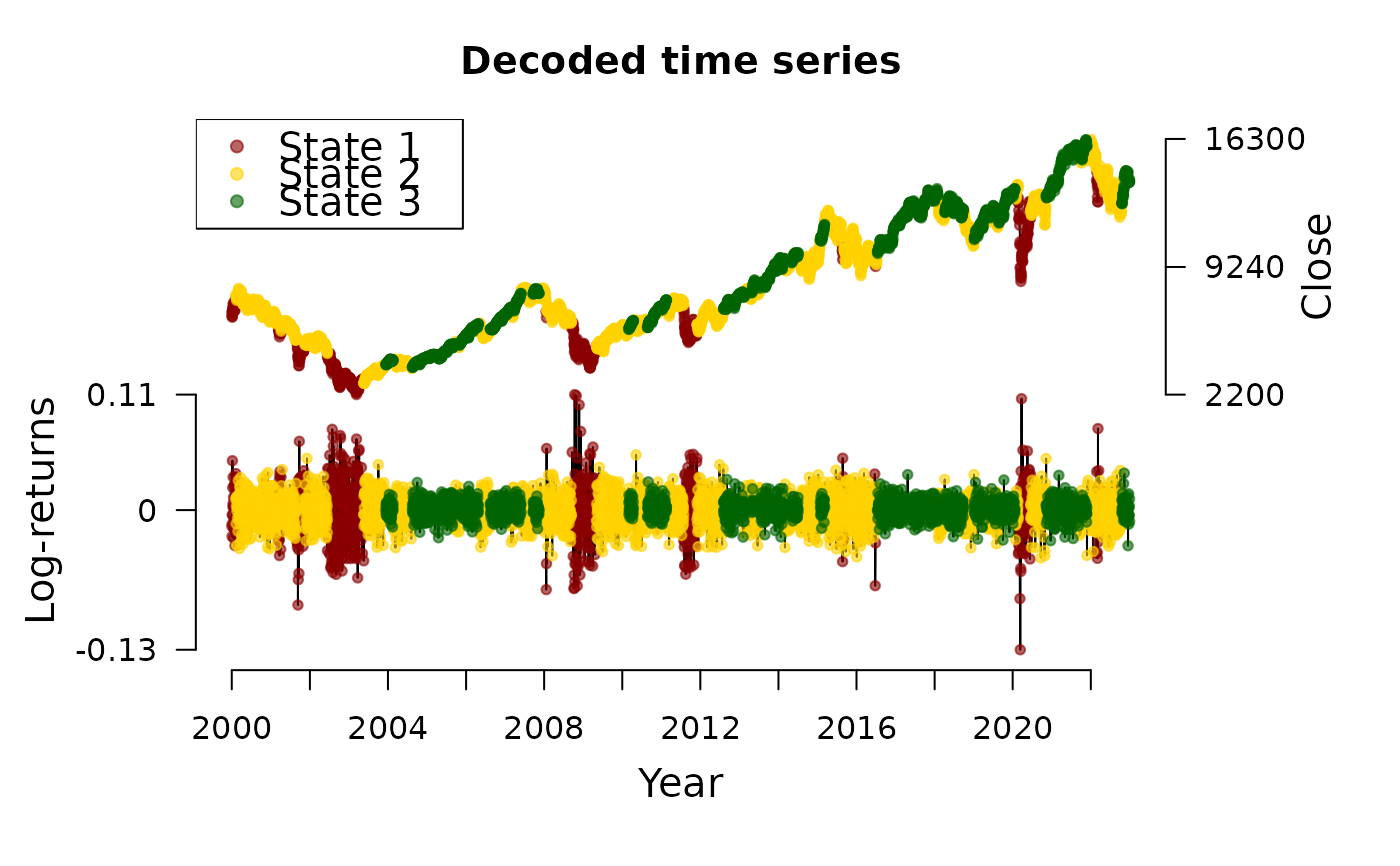
decode_states(dax_model_3t)
#> Decoded states
#> fHMM fitted model:
#> * total estimation time: 3 mins 
#> * accepted runs: 100 of 100 
#> * log-likelihood: 17650.02 
plot(dax_model_3t, type = "ts")

viterbi(
  observations = c(1, 1, 1, 10, 10, 10),
  nstates      = 2,
  sdd          = "poisson",
  Gamma        = matrix(0.5, 2, 2),
  mu           = c(1, 10)
)
#> [1] 1 1 1 2 2 2