Skip to contents

Model fitting

Source: R/fit_model.R
fit_model.Rd

This function fits a hidden Markov model via numerical likelihood maximization.

Usage

fit_model(
  data,
  controls = data[["controls"]],
  fit = list(),
  runs = 10,
  origin = FALSE,
  accept = 1:3,
  gradtol = 0.01,
  iterlim = 100,
  print.level = 0,
  steptol = 0.01,
  ncluster = 1,
  seed = NULL,
  verbose = TRUE,
  initial_estimate = NULL
)

Arguments

data

An object of class fHMM_data.

controls

Either a list or an object of class fHMM_controls.

The list can contain the following elements, which are described in more detail below:

  • hierarchy, defines an hierarchical HMM,

  • states, defines the number of states,

  • sdds, defines the state-dependent distributions,

  • horizon, defines the time horizon,

  • period, defines a flexible, periodic fine-scale time horizon,

  • data, a list of controls that define the data,

  • fit, a list of controls that define the model fitting

Either none, all, or selected elements can be specified.

Unspecified parameters are set to their default values.

Important: Specifications in controls always override individual specifications.

fit

A list of controls specifying the model fitting.

The list can contain the following elements, which are described in more detail below:

  • runs, defines the number of numerical optimization runs,

  • origin, defines initialization at the true parameters,

  • accept, defines the set of accepted optimization runs,

  • gradtol, defines the gradient tolerance,

  • iterlim, defines the iteration limit,

  • print.level, defines the level of printing,

  • steptol, defines the minimum allowable relative step length.

Either none, all, or selected elements can be specified.

Unspecified parameters are set to their default values, see below.

Specifications in fit override individual specifications.

runs

An integer, setting the number of randomly initialized optimization runs of the model likelihood from which the best one is selected as the final model.

By default, runs = 10.

origin

Only relevant for simulated data, i.e., if the data control is NA.

In this case, a logical. If origin = TRUE the optimization is initialized at the true parameter values. This sets run = 1 and accept = 1:5.

By default, origin = FALSE.

accept

An integer (vector), specifying which optimization runs are accepted based on the output code of nlm.

By default, accept = 1:3.

gradtol

A positive numeric value, specifying the gradient tolerance, passed on to nlm.

By default, gradtol = 0.01.

iterlim

A positive integer value, specifying the iteration limit, passed on to nlm.

By default, iterlim = 100.

print.level

One of 0, 1, and 2 to control the verbosity of the numerical likelihood optimization, passed on to nlm.

By default, print.level = 0.

steptol

A positive numeric value, specifying the step tolerance, passed on to nlm.

By default, gradtol = 0.01.

ncluster

Set the number of clusters for parallel optimization runs to reduce optimization time. By default, ncluster = 1 (no clustering).

seed

Set a seed for the generation of initial values. No seed by default.

verbose

Set to TRUE to print progress messages.

initial_estimate

Optionally defines an initial estimate for the numerical likelihood optimization. Good initial estimates can improve the optimization process. Can be:

  • NULL (the default), in this case

    • applies a heuristic to calculate a good initial estimate

    • or uses the true parameter values (if available and data$controls$origin is TRUE)

  • or an object of class parUncon (i.e., a numeric of unconstrained model parameters), for example the estimate of a previously fitted model (i.e. the element model$estimate).

Value

An object of class fHMM_model.

Details

Multiple optimization runs starting from different initial values are computed in parallel if ncluster > 1.

Examples

### 2-state HMM with normal distributions

# set specifications
controls <- set_controls(
  states = 2, sdds = "normal", horizon = 100, runs = 10
)

# define parameters
parameters <- fHMM_parameters(controls, mu = c(-1, 1), seed = 1)

# sample data
data <- prepare_data(controls, true_parameter = parameters, seed = 1)

# fit model
model <- fit_model(data, seed = 1)
#> Checking start values...
#> Maximizing likelihood...
#> Approximating Hessian...
#> Fitting completed!

# inspect fit
summary(model)
#> Summary of fHMM model
#> 
#>   simulated hierarchy        LL      AIC     BIC
#> 1      TRUE     FALSE -62.46497 136.9299 152.561
#> 
#> State-dependent distributions:
#> normal() 
#> 
#> Estimates:
#>                 lb estimate      ub    true
#> Gamma_2.1  0.07297   0.1375  0.2441  0.1632
#> Gamma_1.2  0.14580   0.2638  0.4294  0.3116
#> mu_1      -1.01451  -0.9809 -0.9474 -1.0000
#> mu_2       0.91985   1.0404  1.1609  1.0000
#> sigma_1    0.08018   0.1013  0.1280  0.1008
#> sigma_2    0.41678   0.4954  0.5889  0.6008
plot(model, "sdds")


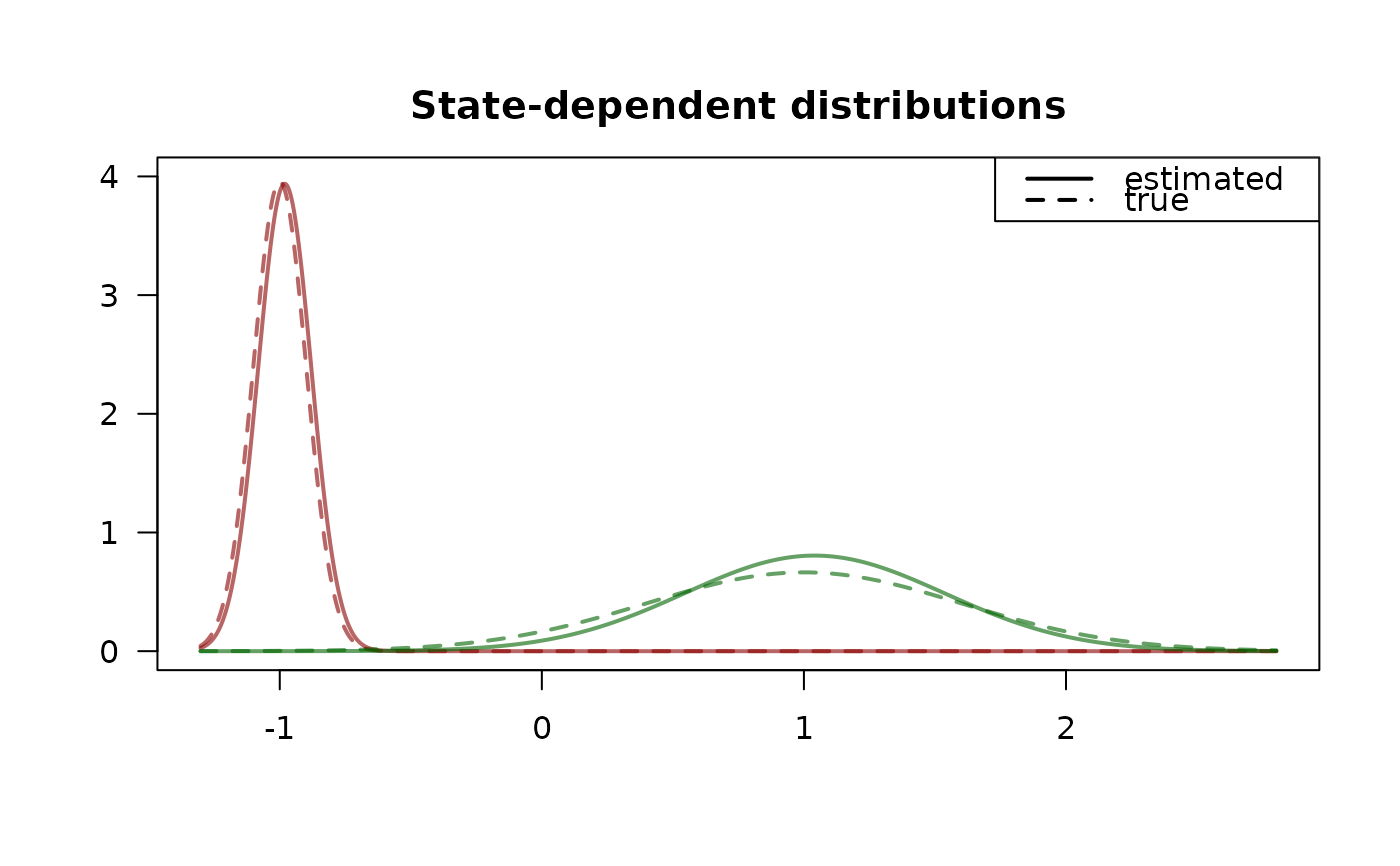# decode states
model <- decode_states(model)
#> Decoded states
plot(model, "ts")


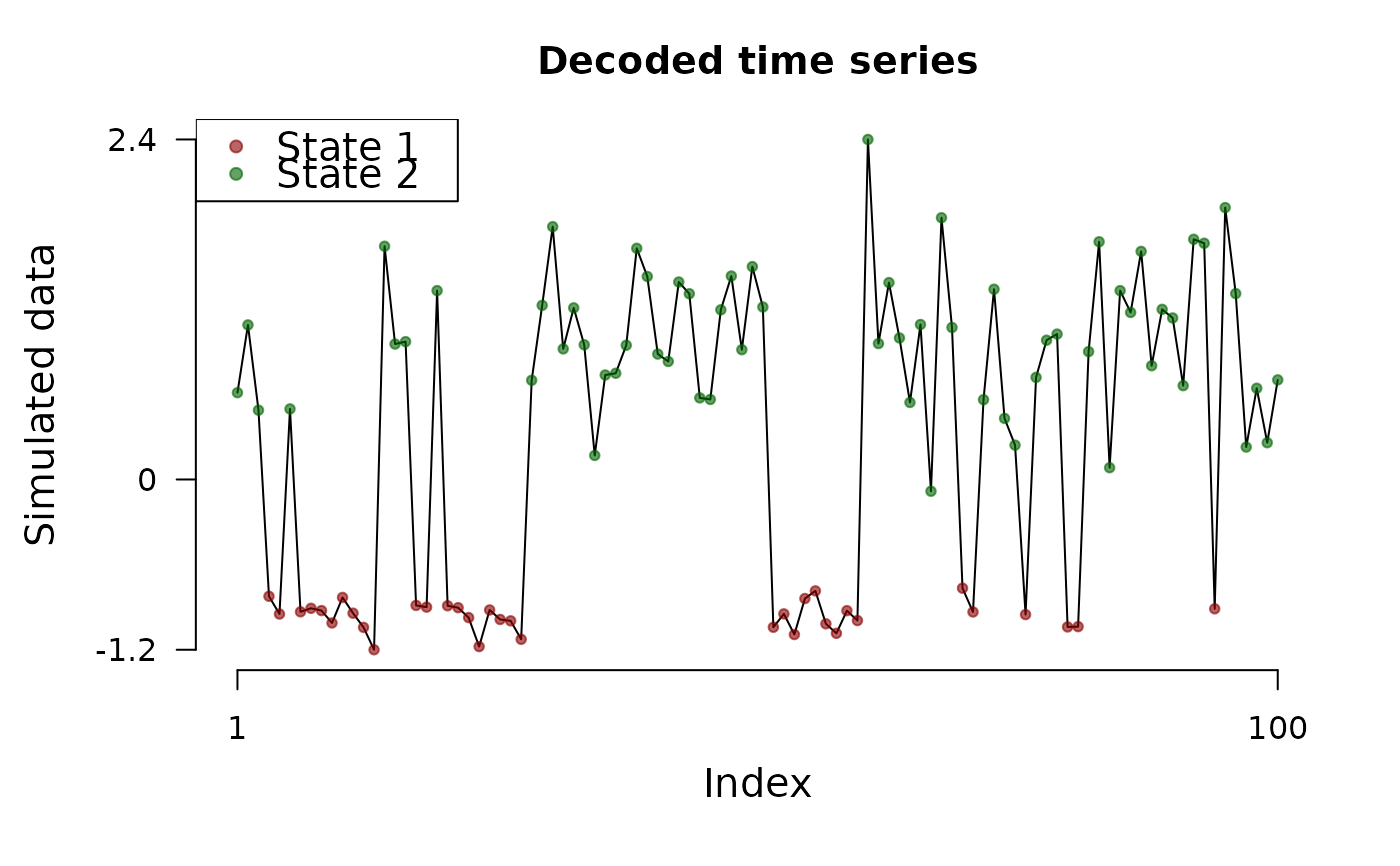# predict
predict(model, ahead = 5)
#>   state_1 state_2       lb estimate      ub
#> 1 0.13749 0.86251  0.03672  0.76246 1.48820
#> 2 0.21980 0.78020 -0.07631  0.59608 1.26846
#> 3 0.26909 0.73091 -0.14397  0.49647 1.13691
#> 4 0.29859 0.70141 -0.18448  0.43683 1.05815
#> 5 0.31625 0.68375 -0.20874  0.40113 1.01099