Skip to contents

Choice data

Source: vignettes/v02_choice_data.Rmd
v02_choice_data.Rmd

No choice model without choice data, so this vignette1 provides a reference for data management in RprobitB. We use the train_choice data set for illustration.

Requirements to choice data

RprobitB helps in modeling the choice of individual deciders of one alternative from a finite set of choice alternatives. This choice set has to fulfill three properties (Train 2009): Choices need to be

  1. mutually exclusive (one can choose one and only one alternative that are all different),

  2. exhaustive (the alternatives do not leave other options open),

  3. and finitely many.

Every decider may take one or repeated choices (called choice occasions). The data set thus contains information on

  1. an identifier for each decider (and optionally for each choice situation),

  2. the choices,

  3. alternative and decider specific covariates.

Additionally, RprobitB asks the following formal requirements:

  1. The data set must be in “wide” format, that means each row provides the full information for one choice occasion.2

  2. It must contain a column with unique identifiers for each decision maker. Additionally, it can contain a column with identifier for each choice situation of each decider. If this information is missing, these identifier are generated automatically by the appearance of the choices in the data set.3

  3. It can contain a column with the observed choices. Such a column is required for model fitting but not for prediction.

  4. It must contain columns for the values of each alternative specific covariate for each alternative and for each decider specific covariate.

Example

The train_choice data set contains 2929 stated choices by 235 Dutch individuals deciding between two virtual train trip options based on the price, the travel time, the level of comfort, and the number of changes. It fulfills the above requirements: Each row represents one choice occasion, the columns id and choiceid identify the deciders and the choice occasions, respectively. The column choice gives the observed choices. Four alternative-specific covariates are available, namely price, time, change, and comfort. There values are given for each alternative.4

str(train_choice)
#> 'data.frame':    2929 obs. of  11 variables:
#>  $ deciderID : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ occasionID: int  1 2 3 4 5 6 7 8 9 10 ...
#>  $ choice    : chr  "A" "A" "A" "B" ...
#>  $ price_A   : num  52.9 52.9 52.9 88.1 52.9 ...
#>  $ time_A    : num  2.5 2.5 1.92 2.17 2.5 ...
#>  $ change_A  : int  0 0 0 0 0 0 0 0 0 0 ...
#>  $ comfort_A : int  1 1 1 1 1 0 1 1 0 1 ...
#>  $ price_B   : num  88.1 70.5 88.1 70.5 70.5 ...
#>  $ time_B    : num  2.5 2.17 1.92 2.5 2.5 ...
#>  $ change_B  : int  0 0 0 0 0 0 0 0 0 0 ...
#>  $ comfort_B : int  1 1 0 0 0 0 1 0 1 0 ...

The model formula

We have to inform RprobitB about the covariates we want to include in our model via specifying a formula object. Say we want to model the utility \(U_{n,t,j}\) of decider \(n\) at choice occasion \(t\) for alternative \(j\) via the linear equation

\[U_{n,t,j} = A_{n,t,j} \beta_1 + B_{n,t} \beta_{2,j} + C_{n,t,j} \beta_{3,j} + \epsilon_{n,tj}.\] Here, \(A\) and \(C\) are alternative and choice situation specific covariates, whereas \(B\) is choice situation specific. The coefficient \(\beta_1\) is generic (i.e. the same for each alternative), whereas \(\beta_{2,j}\) and \(\beta_{3,j}\) are alternative specific.

To represent this structure, the formula object is of the form (analogously to mlogit) choice ~ A | B | C, where

  • choice is the dependent variable (the discrete choice we aim to explain),

  • A are alternative and choice situation specific covariates with a generic coefficient (we call them covariates of type 1),

  • B are choice situation specific covariates with alternative specific coefficients5 (we call them covariates of type 2),

  • and C are alternative and choice situation specific covariates with alternative specific coefficients (we call them covariates of type 3).

Specifying a formula object for RprobitB must be consistent with the following rules:

  • By default, alternative specific constants (ASCs)6 are added to the model. They can be removed by adding + 0 in the second spot, e.g. choice ~ A | B + 0 | C.

  • To exclude covariates of the backmost categories, use either 0, e.g. choice ~ A | B | 0 or just leave this part out and write choice ~ A | B. However, to exclude covariates of front categories, we have to use 0, e.g. choice ~ 0 | B.

  • To include more than one covariate of the same category, use +, e.g. choice ~ A1 + A2 | B.

  • If we don’t want to include any covariates of the second category but we want to estimate alternative specific constants, add 1 in the second spot, e.g. choice ~ A | 1. The expression choice ~ A | 0 is interpreted as no covariates of the second category and no alternative specific constants.

To impose random effects for specific variables, we need to define a character vector re with the corresponding variable names. To have random effects for the alternative specific constants, include "ASC" in re.

Example

We specify a model formula for the train_choice data set. Say we want to include all the covariates price, time, comfort, and change, which are all alternative specific (that is, they contain a potentially different value for each alternative, such as different prices for A and B), so either of type 1 or type 3. The difference between type 1 and type 3 is that in the former case, we would estimate a generic coefficient (i.e. a coefficient that is constant across alternatives), whereas in the latter case, we would estimate alternative specific coefficients. Deciding between type 1 and type 3 for these covariates belongs into the topic of model selection, for which we provide a separate vignette. For now, we go with type 1 for all covariates and remove ASCs:

form <- choice ~ price + time + comfort + change | 0

Additionally, we specify random effects for price and time (because we would typically expect heterogeneity here):

re <- c("price", "time")

The prepare_data() function

Before model estimation with RprobitB, any empirical choice data set choice_data must pass the prepare_data() function:

data <- prepare_data(form = form, choice_data = choice_data)

The function performs compatibility checks and data transformations and returns an object of class RprobitB_data that can be fed into the estimation routine fit_model(). The following arguments are optional:

  • re: The character vector of variable names of form with random effects. re = NULL per default, i.e. no random effects.

  • alternatives: We may not want to consider all alternatives in choice_data. In that case, we can specify a character vector alternatives with selected names of alternatives. If not specified, the choice set is defined by the observed choices.

  • id: A character (single string), the name of the column in choice_data that contains a unique identifier for each decision maker. The default is "id".

  • idc: A character, the name of the column in choice_data that contains a unique identifier for each choice situation given the decision maker. Per default, these identifier are generated by the appearance of the choices in the data set.

  • standardize: A character vector of variable names of form that get standardized. Covariates of type 1 or 3 have to be addressed by <covariate>_<alternative>. If standardize = "all", all covariates get standardized. Per default, no covariate is standardized.

  • impute: Specifies how to handle missing entries (NA, NaN, -Inf, Inf) in choice_data. The following options are available:

    • "complete_cases", which removes rows containing missing entries (the default),

    • "zero", which replaces missing entries by zero,

    • "mean", which imputes missing entries by the covariate mean.

Example

Let’s prepare the train_choice data set for estimation with our previous specification of form and re:

data <- prepare_data(form = form, choice_data = train_choice, re = re, id = "deciderID", idc = "occasionID")

The summary and plot methods provide a quick data overview:

summary(data)
#>                  count
#> deciders           235
#> choice occasions  5-19
#> total choices     2929
#> alternatives         2
#> - 'A'             1474
#> - 'B'             1455
plot(data)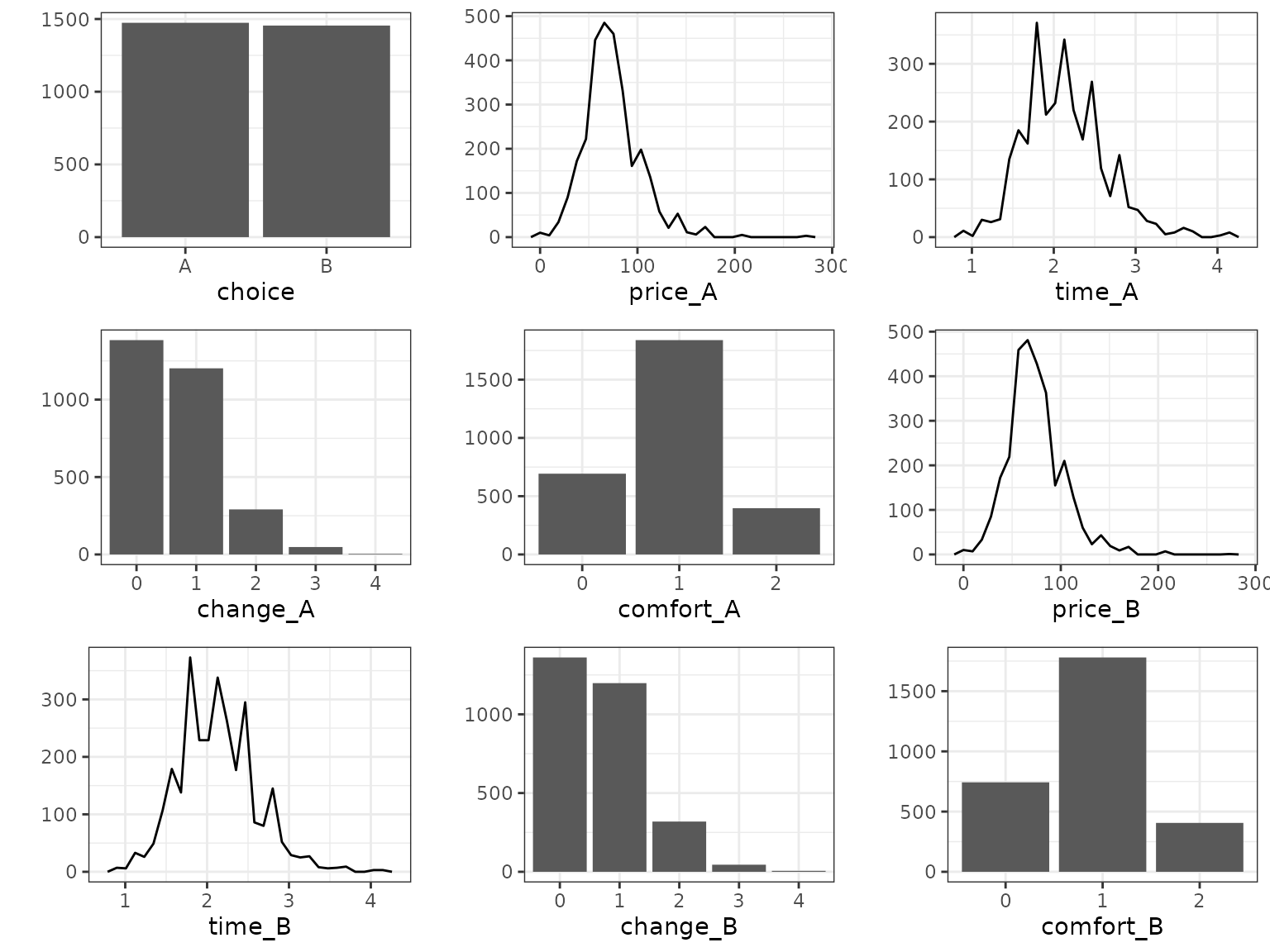

Ordered alternatives

The two choice alternatives from the train trip example are unordered. If we had asked “rate your train trip from 1 (horrible) to 7 (great)”, then the respondents would choose from a set of ordered alternatives. Such ordered alternatives can by analyzed by setting ordered = TRUE in prepare_data. In this case, alternatives becomes a mandatory argument, where the alternatives must be named from worst to best.

Ranked choices

Rather than recording only the single most preferred alternative, some surveys ask for a full ranking of all the alternatives, which reveals far more about the underlying preferences. Ranked choices can by analyzed by setting ranked = TRUE in prepare_data(). The choice column of the data set must provide the full ranking for each choice occasion (from most preferred to least preferred), where the alternatives are separated by commas.

The ranked probit model follows directly from the basic multivariate case. The only difference is that we take flexible utility differences such that the differenced utility vector is always negative. Thereby, we incorporate information of the full ranking.

Simulate choices

The simulate_choices function simulates discrete choice data from a prespecified probit model. Say we want to simulate the choices of N deciders in T choice occasions7 among J alternatives from a model formulation form, we have to call

data <- simulate_choices(form = form, N = N, T = T, J = J)

The function simulate_choices() has the following optional arguments:

  • re: The character vector of variable names of form with random effects.

  • alternatives: A character vector of length J with the names of the choice alternatives. If not specified, the alternatives are labeled by the first J upper-case letters of the Roman alphabet.

  • covariates: A named list of covariate values. Each element must be a vector of length equal to the number of choice occasions and named according to a covariate, or follow the naming convention for alternative specific covariates, i.e. <covariate>_<alternative>. Covariates for which no values are specified are drawn from a standard normal distribution.

  • standardize: A character vector of variable names of form that get standardized.

  • seed: Set a seed for the simulation.

We can specify the true parameters8 by adding a named list with values for

  • alpha, the fixed coefficient vector,

  • C, the number (greater or equal 1) of latent classes of decision makers,

  • s, the vector of class weights,

  • b, the matrix of class means as columns,

  • Omega, the matrix of class covariance matrices as columns,

  • Sigma, the differenced error term covariance matrix, or Sigma_full, the full error term covariance matrix,

  • beta, the matrix of the decision-maker specific coefficient vectors,

  • z, the class allocation vector,

  • d, the vector of logarithmic threshold increments in the ordered probit case.

True parameters that are not specified will be set at random.

Example

For illustration, we simulate the choices of N = 100 deciders at T = 10 choice occasions between the alternatives A and B:

N <- 100
T <- 10
alternatives <- c("A", "B")
base <- "B"
form <- choice ~ var1 | var2 | var3
re <- c("ASC", "var2")

RprobitB provides the function overview_effects() which can be used to get an overview of the effects for which parameters can be specified:

overview_effects(form = form, re = re, alternatives = alternatives, base = base)
#>   effect as_value as_coef random
#> 1   var1     TRUE   FALSE  FALSE
#> 2 var3_A     TRUE    TRUE  FALSE
#> 3 var3_B     TRUE    TRUE  FALSE
#> 4 var2_A    FALSE    TRUE   TRUE
#> 5  ASC_A    FALSE    TRUE   TRUE

Hence, the coefficient vector alpha must be of length 3, where the elements 1 to 3 correspond to var1, var3_A, and var3_B, respectively. The matrix b must be of dimension 2 x C, where (by default) C = 1 and row 1 and 2 correspond to var2_A and ASC_A, respectively.

data <- simulate_choices(
  form = form,
  N = N,
  T = T,
  J = 2,
  re = re,
  alternatives = alternatives,
  seed = 1,
  true_parameter = list(
    alpha = c(-1, 0, 1),
    b = matrix(c(2, -0.5), ncol = 1)
  )
)
summary(data)
#>                  count
#> deciders           100
#> choice occasions    10
#> total choices     1000
#> alternatives         2
#> - 'A'              435
#> - 'B'              565

We can visualize the covariates grouped by the chosen alternatives:

plot(data, by_choice = TRUE)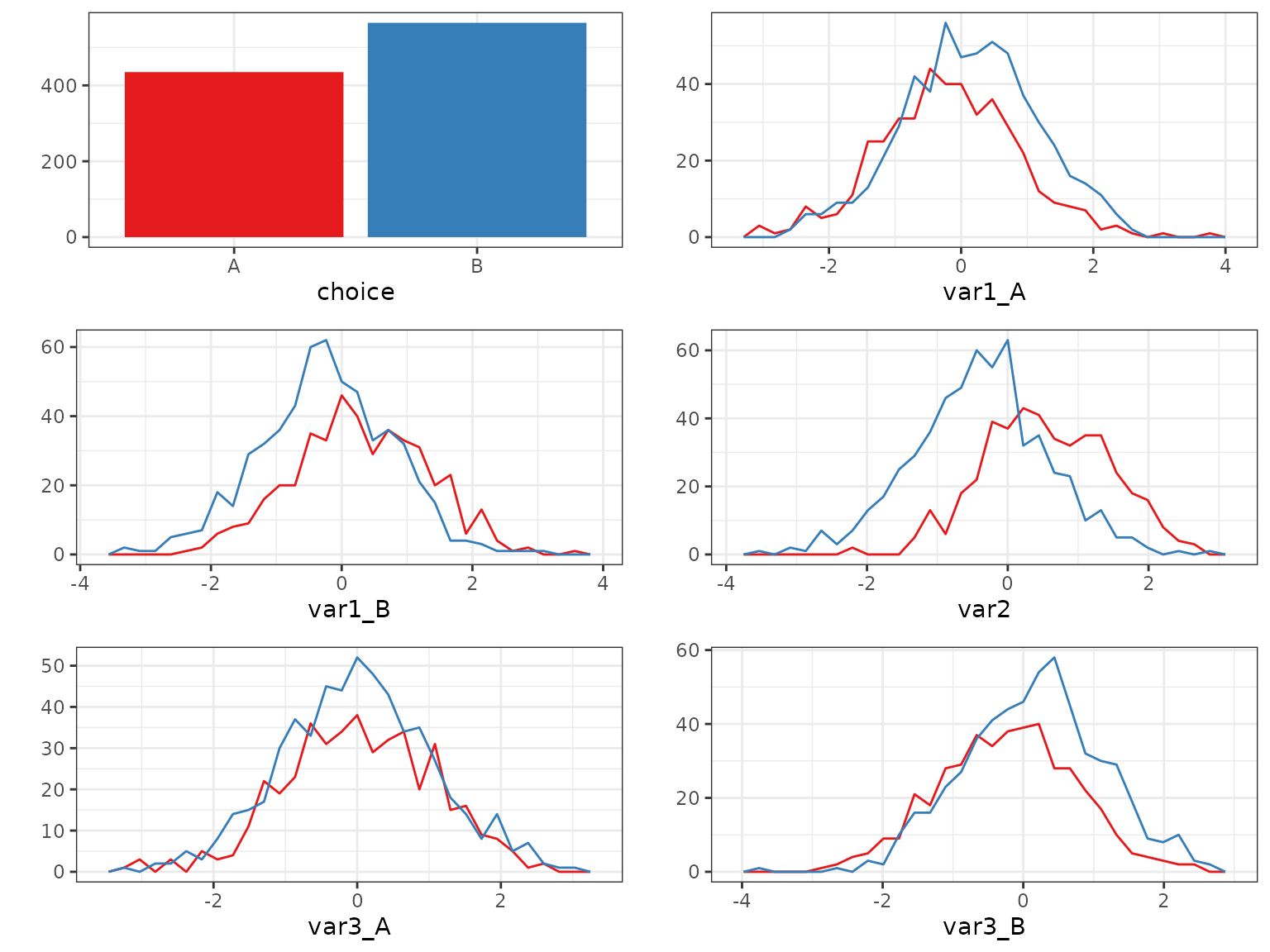

What we see is consistent with our specification: Higher values of var1_A for example correspond more frequently to choice B (upper-right panel), because the coefficient of var1 (the first value of alpha) is negative.

Train and test data set

The function train_test() can be used to split the output of prepare_data() or simulate_choices() into a train and a test subset. This is useful when evaluating the prediction performance of a fitted model. For example, the following code puts 70% of deciders from our simulated data into the train subsample and 30% of deciders in the test subsample:

train_test(data, test_proportion = 0.3, by = "N")
#> $train
#> Simulated data of 700 choices.
#> 
#> $test
#> Simulated data of 300 choices.

Alternatively, the following code puts 2 randomly chosen choice occasions per decider from data into the test subsample, the rest goes into the train subsample:

train_test(data, test_number = 2, by = "T", random = TRUE, seed = 1)
#> $train
#> Simulated data of 800 choices.
#> 
#> $test
#> Simulated data of 200 choices.

References

Train, K. 2009. Discrete Choice Methods with Simulation. Cambridge University Press. https://doi.org/10.1017/CBO9780511805271.