This vignette1 discusses in-sample and out-of-sample prediction within RprobitB. The former case refers to reproducing the observed choices on the basis of the covariates and the fitted model and subsequently using the deviations between prediction and reality as an indicator for the model performance. The latter means forecasting choice behavior for changes in the choice attributes.
For illustration, we revisit the probit model of travelers deciding between two fictional train route alternatives from the vignette on model fitting:
form <- choice ~ price + time + change + comfort | 0
data <- prepare_data(form = form, choice_data = train_choice, id = "deciderID", idc = "occasionID")
model_train <- fit_model(
data = data,
scale = "price := -1"
)Reproducing the observed choices
RprobitB provides a predict() method for
RprobitB_fit objects. Per default, the method returns a
confusion matrix, which gives an overview of the in-sample prediction
performance:
predict(model_train)
#> predicted
#> true A B
#> A 1035 439
#> B 448 1007By setting the argument overview = FALSE, the method
instead returns predictions on the level of individual choice
occasions:
pred <- predict(model_train, overview = FALSE)
head(pred, n = 10)
#> deciderID occasionID A B true predicted correct
#> 1 1 1 0.91 0.09 A A TRUE
#> 2 1 2 0.64 0.36 A A TRUE
#> 3 1 3 0.79 0.21 A A TRUE
#> 4 1 4 0.18 0.82 B B TRUE
#> 5 1 5 0.55 0.45 B A FALSE
#> 6 1 6 0.13 0.87 B B TRUE
#> 7 1 7 0.54 0.46 B A FALSE
#> 8 1 8 0.76 0.24 B A FALSE
#> 9 1 9 0.55 0.45 A A TRUE
#> 10 1 10 0.59 0.41 A A TRUEAmong the three incorrect predictions shown here, the one for decider
id = 1 in choice occasion idc = 8 is the most
outstanding. Alternative B was chosen although the model
predicts a probability of 76% for alternative A. We can use
the helper function get_cov() to extract the
characteristics of this particular choice situation:
get_cov(model_train, id = 1, idc = 8)
#> deciderID occasionID choice price_A time_A change_A comfort_A price_B
#> 8 1 8 B 52.88904 1.916667 0 1 70.51872
#> time_B change_B comfort_B
#> 8 2.5 0 0The trip option A was 20€ cheaper and 30 minutes faster,
which by our model outweighs the better comfort class for alternative
B, recall the estimated effects:
coef(model_train)
#> Estimate (sd)
#> 1 price -1.00 (0.00)
#> 2 time -25.94 (2.20)
#> 3 change -4.96 (0.85)
#> 4 comfort -14.50 (0.91)The misclassification can be explained by preferences that differ from the average decider (choice behaviour heterogeneity), or by unobserved factors that influenced the choice. Indeed, the variance of the error term was estimated high:
point_estimates(model_train)$Sigma
#> [,1]
#> [1,] 660.3985
#> attr(,"names")
#> [1] "1,1"Apart from the prediction accuracy, the model performance can be evaluated more nuanced in terms of sensitivity and specificity. The following snippet exemplary shows how to visualize these measures by means of a receiver operating characteristic (ROC) curve (Fawcett 2006), comparing the prediction performance to a model that only uses the price as explanatory variable:
model_train_basic <- update(model_train, form = choice ~ price | 0)
plot_roc(model_train, model_train_basic)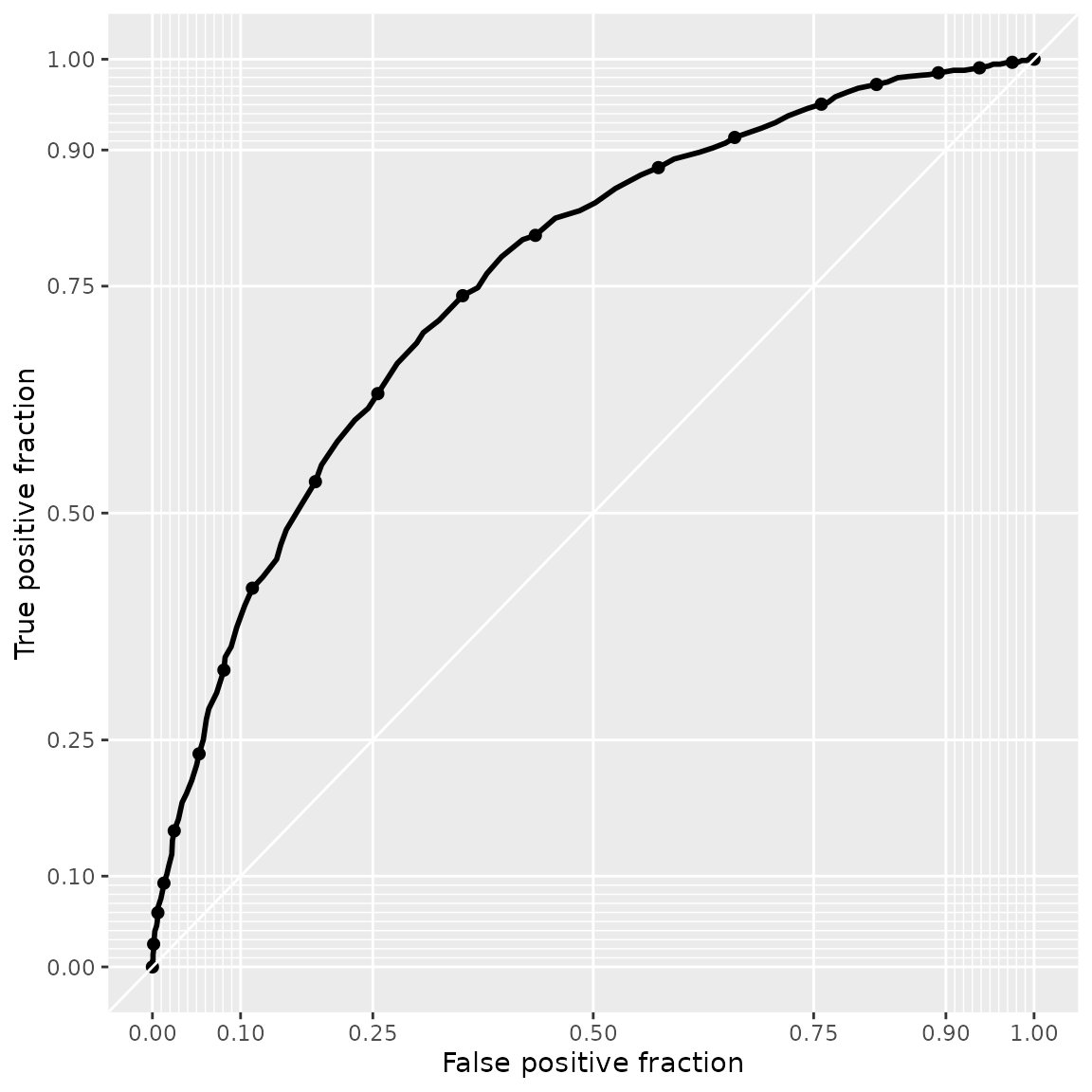
The prediction performance of model_train is better,
because its ROC curve lies above.
Forecasting choice behavior
The predict() method has an additional data
argument. Per default, data = NULL, which results into the
in-sample case outlined above. Alternatively, data can be
either
an
RprobitB_dataobject (for example the test subsample derived from thetrain_test()function, see the vignette on choice data),or a data frame of custom choice characteristics.
We demonstrate the second case in the following. Assume that a train company wants to anticipate the effect of a price increase on their market share. By our model, increasing the ticket price from 100€ to 110€ (ceteris paribus) draws 15% of the customers to the competitor who does not increase their prices.
predict(
model_train,
data = data.frame(
"price_A" = c(100, 110),
"price_B" = c(100, 100)
),
overview = FALSE
)
#> deciderID occasionID A B prediction
#> 1 1 1 0.50 0.50 A
#> 2 2 1 0.35 0.65 BHowever, offering a better comfort class compensates for the higher price and even results in a gain of 7% market share:
